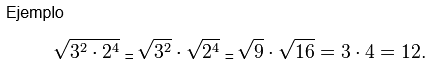NÚMEROS REALES

 

NÚMEROS IRRACIONALES

 Son aquellos números que tienen infinitas cifras decimales no periódicas, por  tanto NO pueden ser expresados  en la forma  a/b.

Como  ejemplo de número IRRACIONAL,   se tiene  el número  √2  = 1,41421356… Y también todas las raíces  no exactas.

Un número IRRACIONAL muy conocido es el número π, (número Pi), cuya expresión es  π  = 3,14159265….

  NÚMEROS REALES

Resulta de la unión del conjunto de los números racionales con el conjunto de números Irracionales.

El conjunto de los números REALES  se simboliza con la letra R

R = Q ∪ I ,  donde , N ∁ Z ∁ Q

 

La gráfica anterior, nos dice que el conjunto de los reales, contiene a los Naturales, Enteros, Racionales e Irracionales

 

Ejemplo

Analiza a que conjunto numérico pertenece cada elemento

   a)13/4                b)-√6                c)7

Solución:

a) 13/4=1,444…   es un número Racional, tiene infinitas cifras decimales periódicas

b)  -√6 = - 449489473…, es un número Irracional, tiene infinitas cifras decimales no periódicas

c) 7, es un número Natural, entero positivo y por tanto Racional

Todos los números dados son números Reales

 

POTENCIACIÓN DE LOS  NÚMEROS    RALES

 La potenciación es una forma abreviada de escribir una multiplicación de factores iguales

 

Regla de los signos para la potenciación  

 

Propiedades de la potenciación

 

EJEMPLOS

Ø  1.- (0,25)¹  = 0,25          EXPONENTE 1

222.-     (√2)⁰  = 1               EXPONENTE CERO

333.-                   EXPONENTE    NEGATIVO

 

4.-4.-  PRODUCTOS DE IGUAL BASE

 

    5.- EJEMPLO INTERESANTE, EN ÉL SE APLICAN CASI TODAS LAS PROPIEDADES

  

 

 

EJERCICIOS INTERACTIVOS: Intermatia: https://www.intermatia.com/ejercicios/PT003/

RADICACIÓN DE LOS NÚMEROS REALES

Es una operación inversa a la potenciación en la que se busca la base, conocida el exponente y la potencia

                                              TÉRMINOS EN LA RADICACIÓN  

                                               

 

EJEMPLOS

 

Raíces de un radical  

Exponente fraccionario

Una potencia de exponente fraccionario se puede transformar en una raíz cuyo Índice es el denominador y el radicando es la base elevada al numerador. Por lo tanto al resolver una potencia con exponente fraccionario quedaría:

 

 

Esta propiedad se utiliza para simplificar  potencias y radicales

Ejemplos 

 

 

 

 

 

 

Propiedades de la radicación

La raíz de un producto es igual al producto de las raíces de los factores: 

La raíz de una fracción es igual al cociente de la raíz del numerador entre la raíz del denominador: 

 

 

RAIZ DE UNA RAIZ

PARA SABER MÀS: https://www.profesorenlinea.cl/matematica/Raiz_de_radical.html